BornAgain  1.19.79
Open-source research software to simulate and fit neutron and x-ray reflectometry and grazing-incidence small-angle scattering
Probability Density Functions (PDF)
Statistical functions

Description

Probability density functions of various statistical distributions (continuous and discrete). The probability density function returns the probability that the variate has the value x. In statistics the PDF is also called the frequency function.

Collaboration diagram for Probability Density Functions (PDF):

Probability Density Functions from MathCore

Additional PDF's are provided in the MathMore library (see PDF functions from MathMore)

double ROOT::Math::beta_pdf (double x, double a, double b)
 
double ROOT::Math::binomial_pdf (unsigned int k, double p, unsigned int n)
 
double ROOT::Math::negative_binomial_pdf (unsigned int k, double p, double n)
 
double ROOT::Math::breitwigner_pdf (double x, double gamma, double x0=0)
 
double ROOT::Math::cauchy_pdf (double x, double b=1, double x0=0)
 
double ROOT::Math::chisquared_pdf (double x, double r, double x0=0)
 
double ROOT::Math::crystalball_function (double x, double alpha, double n, double sigma, double x0=0)
 
double ROOT::Math::exponential_pdf (double x, double lambda, double x0=0)
 
double ROOT::Math::fdistribution_pdf (double x, double n, double m, double x0=0)
 
double ROOT::Math::gamma_pdf (double x, double alpha, double theta, double x0=0)
 
double ROOT::Math::gaussian_pdf (double x, double sigma=1, double x0=0)
 
double ROOT::Math::bigaussian_pdf (double x, double y, double sigmax=1, double sigmay=1, double rho=0, double x0=0, double y0=0)
 
double ROOT::Math::landau_pdf (double x, double xi=1, double x0=0)
 
double ROOT::Math::lognormal_pdf (double x, double m, double s, double x0=0)
 
double ROOT::Math::normal_pdf (double x, double sigma=1, double x0=0)
 
double ROOT::Math::poisson_pdf (unsigned int n, double mu)
 
double ROOT::Math::tdistribution_pdf (double x, double r, double x0=0)
 
double ROOT::Math::uniform_pdf (double x, double a, double b, double x0=0)
 
double ROOT::Math::crystalball_pdf (double x, double alpha, double n, double sigma, double x0=0)
 

Function Documentation

◆ beta_pdf()

double ROOT::Math::beta_pdf ( double  x,
double  a,
double  b 
)

Probability density function of the beta distribution.

\[ p(x) = \frac{\Gamma (a + b) } {\Gamma(a)\Gamma(b) } x ^{a-1} (1 - x)^{b-1} \]

for $0 \leq x \leq 1 $. For detailed description see Mathworld.

◆ bigaussian_pdf()

double ROOT::Math::bigaussian_pdf ( double  x,
double  y,
double  sigmax = 1,
double  sigmay = 1,
double  rho = 0,
double  x0 = 0,
double  y0 = 0 
)

Probability density function of the bi-dimensional (Gaussian) distribution.

\[ p(x) = {1 \over 2 \pi \sigma_x \sigma_y \sqrt{1-\rho^2}} \exp (-(x^2/\sigma_x^2 + y^2/\sigma_y^2 - 2 \rho x y/(\sigma_x\sigma_y))/2(1-\rho^2)) \]

For detailed description see Mathworld. It can also be evaluated using normal_pdf which will call the same implementation.

Parameters
rhocorrelation , must be between -1,1

◆ binomial_pdf()

double ROOT::Math::binomial_pdf ( unsigned int  k,
double  p,
unsigned int  n 
)

Probability density function of the binomial distribution.

\[ p(k) = \frac{n!}{k! (n-k)!} p^k (1-p)^{n-k} \]

for $ 0 \leq k \leq n $. For detailed description see Mathworld.

◆ breitwigner_pdf()

double ROOT::Math::breitwigner_pdf ( double  x,
double  gamma,
double  x0 = 0 
)

Probability density function of Breit-Wigner distribution, which is similar, just a different definition of the parameters, to the Cauchy distribution (see cauchy_pdf )

\[ p(x) = \frac{1}{\pi} \frac{\frac{1}{2} \Gamma}{x^2 + (\frac{1}{2} \Gamma)^2} \]

◆ cauchy_pdf()

double ROOT::Math::cauchy_pdf ( double  x,
double  b = 1,
double  x0 = 0 
)

Probability density function of the Cauchy distribution which is also called Lorentzian distribution.

\[ p(x) = \frac{1}{\pi} \frac{ b }{ (x-m)^2 + b^2} \]

For detailed description see Mathworld. It is also related to the breitwigner_pdf which will call the same implementation.

◆ chisquared_pdf()

double ROOT::Math::chisquared_pdf ( double  x,
double  r,
double  x0 = 0 
)

Probability density function of the $\chi^2$ distribution with $r$ degrees of freedom.

\[ p_r(x) = \frac{1}{\Gamma(r/2) 2^{r/2}} x^{r/2-1} e^{-x/2} \]

for $x \geq 0$. For detailed description see Mathworld.

◆ crystalball_function()

double ROOT::Math::crystalball_function ( double  x,
double  alpha,
double  n,
double  sigma,
double  x0 = 0 
)

Crystal ball function

See the definition at Wikipedia.

It is not really a pdf since it is not normalized

◆ crystalball_pdf()

double ROOT::Math::crystalball_pdf ( double  x,
double  alpha,
double  n,
double  sigma,
double  x0 = 0 
)

pdf definition of the crystal_ball which is defined only for n > 1 otherwise integral is diverging

◆ exponential_pdf()

double ROOT::Math::exponential_pdf ( double  x,
double  lambda,
double  x0 = 0 
)

Probability density function of the exponential distribution.

\[ p(x) = \lambda e^{-\lambda x} \]

for x>0. For detailed description see Mathworld.

◆ fdistribution_pdf()

double ROOT::Math::fdistribution_pdf ( double  x,
double  n,
double  m,
double  x0 = 0 
)

Probability density function of the F-distribution.

\[ p_{n,m}(x) = \frac{\Gamma(\frac{n+m}{2})}{\Gamma(\frac{n}{2}) \Gamma(\frac{m}{2})} n^{n/2} m^{m/2} x^{n/2 -1} (m+nx)^{-(n+m)/2} \]

for x>=0. For detailed description see Mathworld.

◆ gamma_pdf()

double ROOT::Math::gamma_pdf ( double  x,
double  alpha,
double  theta,
double  x0 = 0 
)

Probability density function of the gamma distribution.

\[ p(x) = {1 \over \Gamma(\alpha) \theta^{\alpha}} x^{\alpha-1} e^{-x/\theta} \]

for x>0. For detailed description see Mathworld.

◆ gaussian_pdf()

double ROOT::Math::gaussian_pdf ( double  x,
double  sigma = 1,
double  x0 = 0 
)

Probability density function of the normal (Gaussian) distribution.

\[ p(x) = {1 \over \sqrt{2 \pi \sigma^2}} e^{-x^2 / 2\sigma^2} \]

For detailed description see Mathworld. It can also be evaluated using normal_pdf which will call the same implementation.

◆ landau_pdf()

double ROOT::Math::landau_pdf ( double  x,
double  xi = 1,
double  x0 = 0 
)

Probability density function of the Landau distribution:

\[ p(x) = \frac{1}{\xi} \phi (\lambda) \]

with

\[ \phi(\lambda) = \frac{1}{2 \pi i}\int_{c-i\infty}^{c+i\infty} e^{\lambda s + s \log{s}} ds\]

where $\lambda = (x-x_0)/\xi$. For a detailed description see K.S. Kölbig and B. Schorr, A program package for the Landau distribution, Computer Phys. Comm. 31 (1984) 97-111 [Erratum-ibid. 178 (2008) 972]. The same algorithms as in CERNLIB (DENLAN) is used

Parameters
xThe argument 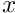$x$
xiThe width parameter 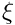$\xi$
x0The location parameter 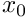$x_0$

◆ lognormal_pdf()

double ROOT::Math::lognormal_pdf ( double  x,
double  m,
double  s,
double  x0 = 0 
)

Probability density function of the lognormal distribution.

\[ p(x) = {1 \over x \sqrt{2 \pi s^2} } e^{-(\ln{x} - m)^2/2 s^2} \]

for x>0. For detailed description see Mathworld.

Parameters
sscale parameter (not the sigma of the distribution which is not even defined)
x0location parameter, corresponds approximately to the most probable value. For x0 = 0, sigma = 1, the x_mpv = -0.22278

◆ negative_binomial_pdf()

double ROOT::Math::negative_binomial_pdf ( unsigned int  k,
double  p,
double  n 
)

Probability density function of the negative binomial distribution.

\[ p(k) = \frac{(k+n-1)!}{k! (n-1)!} p^{n} (1-p)^{k} \]

For detailed description see Mathworld (where $k \to x$ and $n \to r$). The distribution in Wikipedia is defined with a $p$ corresponding to $1-p$ in this case.

◆ normal_pdf()

double ROOT::Math::normal_pdf ( double  x,
double  sigma = 1,
double  x0 = 0 
)

Probability density function of the normal (Gaussian) distribution.

\[ p(x) = {1 \over \sqrt{2 \pi \sigma^2}} e^{-x^2 / 2\sigma^2} \]

For detailed description see Mathworld. It can also be evaluated using gaussian_pdf which will call the same implementation.

◆ poisson_pdf()

double ROOT::Math::poisson_pdf ( unsigned int  n,
double  mu 
)

Probability density function of the Poisson distribution.

\[ p(n) = \frac{\mu^n}{n!} e^{- \mu} \]

For detailed description see Mathworld.

◆ tdistribution_pdf()

double ROOT::Math::tdistribution_pdf ( double  x,
double  r,
double  x0 = 0 
)

Probability density function of Student's t-distribution.

\[ p_{r}(x) = \frac{\Gamma(\frac{r+1}{2})}{\sqrt{r \pi}\Gamma(\frac{r}{2})} \left( 1+\frac{x^2}{r}\right)^{-(r+1)/2} \]

for $k \geq 0$. For detailed description see Mathworld.

◆ uniform_pdf()

double ROOT::Math::uniform_pdf ( double  x,
double  a,
double  b,
double  x0 = 0 
)

Probability density function of the uniform (flat) distribution.

\[ p(x) = {1 \over (b-a)} \]

if $a \leq x<b$ and 0 otherwise. For detailed description see Mathworld.