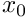Description
Statistical functions for the truncated distributions. Examples of such functions are the first or the second momentum of the truncated distribution. In the case of the Landau, first and second momentum functions are provided for the Landau distribution truncated only on the right side. These functions are defined in the header file Math/ProbFunc.h or in the global one including all statistical functions Math/StatFunc.h
Functions | |
| double | ROOT::Math::landau_xm1 (double x, double xi=1, double x0=0) |
| double | ROOT::Math::landau_xm2 (double x, double xi=1, double x0=0) |
Function Documentation
◆ landau_xm1()
| double ROOT::Math::landau_xm1 | ( | double | x, |
| double | xi = 1, |
||
| double | x0 = 0 |
||
| ) |
First moment (mean) of the truncated Landau distribution.
![]()
where ![]() is the Landau distribution and
is the Landau distribution and ![]() its cumulative distribution function.
its cumulative distribution function.
For detailed description see K.S. Kölbig and B. Schorr, A program package for the Landau distribution, Computer Phys. Comm. 31 (1984) 97-111 [Erratum-ibid. 178 (2008) 972]. The same algorithms as in CERNLIB (XM1LAN) is used
- Parameters
-
x The argument 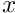
xi The width parameter 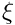
x0 The location parameter 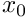
◆ landau_xm2()
| double ROOT::Math::landau_xm2 | ( | double | x, |
| double | xi = 1, |
||
| double | x0 = 0 |
||
| ) |
Second moment of the truncated Landau distribution.
![]()
where ![]() is the Landau distribution and
is the Landau distribution and ![]() its cumulative distribution function.
its cumulative distribution function.
For detailed description see K.S. Kölbig and B. Schorr, A program package for the Landau distribution, Computer Phys. Comm. 31 (1984) 97-111 [Erratum-ibid. 178 (2008) 972]. The same algorithms as in CERNLIB (XM1LAN) is used
- Parameters
-
x The argument 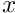
xi The width parameter 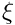
x0 The location parameter