BornAgain ≻ 21 ≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ HemiEllipsoid

HemiEllipsoid

An horizontally oriented ellipsoid, truncated at the central plane.

Constructor

HemiEllipsoid(R_a, R_b, H)

Parameters:

  • R_a, radius $R_{a}$ in $x$ direction
  • R_b, radius $R_{b}$ in $y$ direction
  • H, height

Usage

As for any other Form factor.

Implementation

Class HemiEllipsoid inherits from the interface class IFormFactor .

Computation involves numerical integration in vertical direction,

$$ F(\mathbf{q})=2\pi \int_{0}^H \text{d}z \space r_{a,z} r_{b,z} \frac{J_1(\gamma_{z})}{\gamma_{z}} \thinspace \exp(iq_z z) , $$

with the notation

$$ r_{a,z}:=R_{a}\sqrt{1-\Big( \dfrac{z}{H} \Big)^2}, \quad r_{b,z}:=R_{b}\sqrt{1-\Big( \dfrac{z}{H} \Big)^2}, $$

$$ \quad \gamma_{z} := \sqrt{(q_xr_{a,z})^2 + (q_yr_{b,z})^2}. $$

Volume has been validated against $$ V=\dfrac{2\pi}{3} R_aR_bH. $$

Example

Scattering by uncorrelated, oriented hemiellipsoids for horizontal incidence. Rotation around $z$ axis:

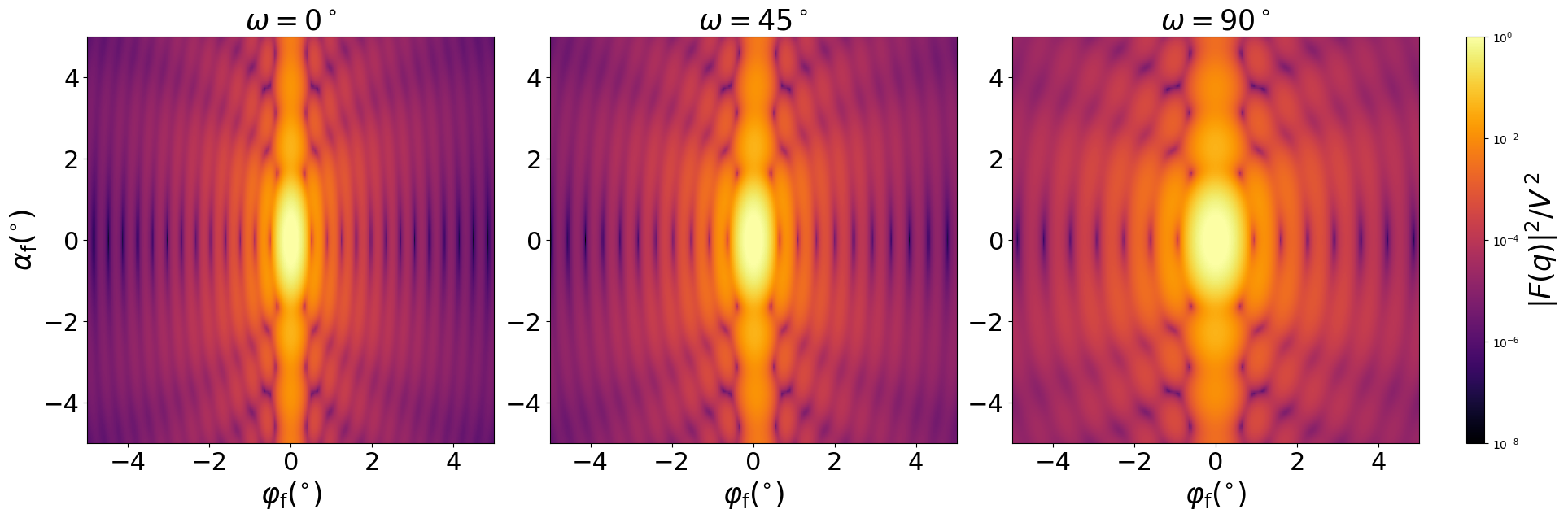
Generated by Examples/ff/HemiEllipsoid.py .

History

Agrees with the IsGISAXS form factor “Anisotropic hemi-ellipsoid” [manual, Eq. 2.41] with wrong sign in the z-dependent phase factor and “Hemi-spheroid” [Renaud 2009, Eq. 229].