 BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ SphericalSegment
BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ SphericalSegment
A spherical segment, obtained from a spherical ball by two parallel cuts.



SphericalSegment(R, t, b)
Parameters:
Constraint:
$ t+b \le 2R $
As for any other Form factor.
Class SphericalSegment inherits from the interface class IFormfactor.
Computation involves numerical integration in vertical direction,
$$ F(\mathbf{q})=2\pi \exp[iq_z(R-b)] \int_{-R+b}^{R-t} \text{d}z \space r_z^2 \frac{J_1(q_{||}r_z)}{q_{||}r_z} \exp(iq_z z), $$
with the notation
$$ q_{||} := \sqrt{q_x^2 + q_y^2}, \quad r_z:=\sqrt{R^2-z^2} $$
Volume has been validated against $$ V=\dfrac{\pi}{3} [ 4R^3 - 3R(t^2+b^2) + (t^3 + b^3) ]. $$
More general:
More special:
Scattering by uncorrelated, oriented truncated spheres for horizontal incidence. Rotation around $y$ axis:
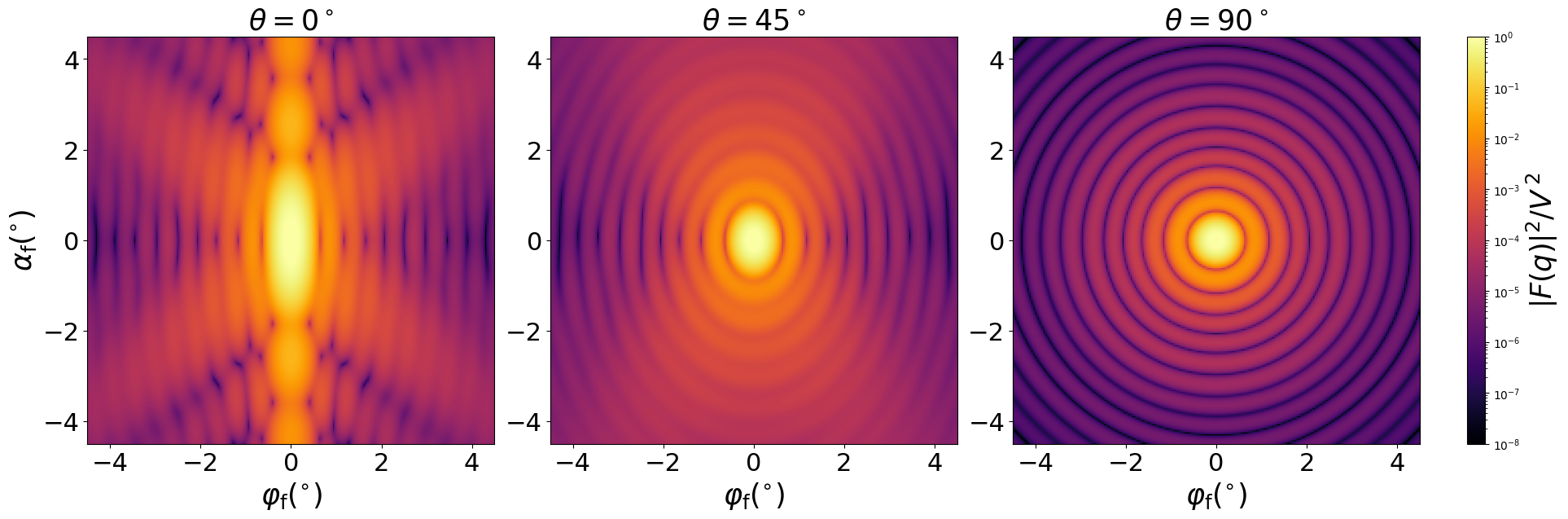
Generated by Examples/ff/SphericalSegment.py .
Agrees with the IsGISAXS form factor “Sphere” [manual, Eq. 2.32] and “Truncated sphere” [Renaud 2009, Eq. 228]. It is not “Truncated sphere” of FitGISAXS, which is without top removal [Babonneau 2013].