 BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ Prism3
BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ Prism3
A prism based on equlateral triangle.



Prism3(L, H)
Parameters:
As for any other Form factor.
Class Prism3 inherits from the interface class IFormfactor .
Form factor is computed as
$$ F(\mathbf{q})=H \space \exp\Big(iq_z\dfrac{H}{2}\Big) \space \text{sinc}\Big(q_z\dfrac{H}{2}\Big) \space F_{||}(\mathbf{q}_{||}) $$
where the form factor $F_{||}(\mathbf{q}_{||}) $ computation is based on the generic form factor of a planar polygon provided by libformfactor .
Volume has been validated against $$ V=\dfrac{\sqrt3}{4}HL^2. $$
More general:
Scattering by uncorrelated, oriented prisms for horizontal incidence. Rotation around $z$ axis:
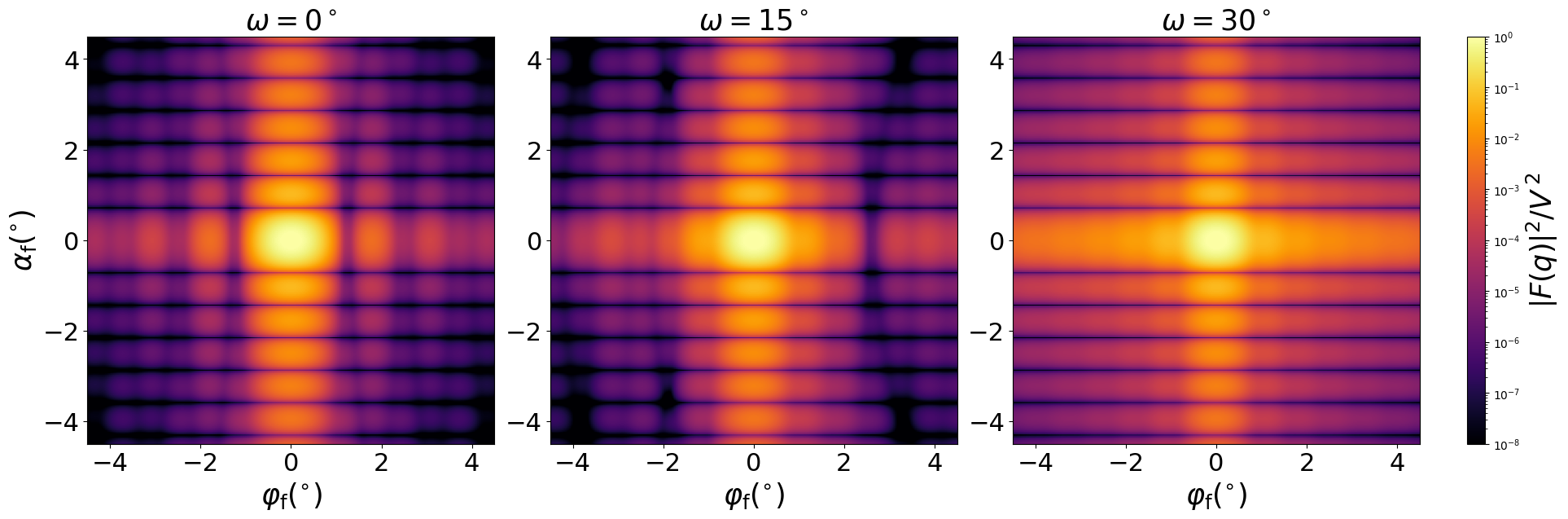
Generated by Examples/ff/Prism3.py .
Has been validated against the “Prism3” form factor of IsGISAXS [manual, Eq. 2.28] and “Prism with three fold symmetry” [Renaud 2009, Eq. 219]. Note the different parametrization $L = 2R_{IsGISXAXS}$. In FitGISAXS [Babonneau 2013] just called “Prism”. In BornAgain 1.6, redefined to let the $x$ axis point along a symmetry axis (rotated by $30^{\circ}$ with respect to the previous version).
Reimplemented in BornAgain 1.6 using the generic form factor of a polygonal prism [Wuttke 2021] to achieve numerical stability near the removable singularity at $q \to 0$.