BornAgain ≻ git-main ≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Ripples ≻ Sawtooth ripple

Sawtooth ripple

A ripple with an asymmetric saw-tooth profile that is uniform in $x$-direction.

Constructor

SawtoothRippleBox(L, W, H, d)
SawtoothRippleGauss(L, W, H, d)
SawtoothRippleLorentz(L, W, H, d)

Parameters:

  • L, length
  • W, width
  • H, height
  • d, asymmetry

Constraint:

$ |d| \le W/2 $

Usage

As for any other Form factor.

Implementation

Class SawtoothRipple inherits from the interface class IFormfactor .

Form factor is computed as

$$ F(\mathbf{q}) = f_\parallel(q_x) f_\bot(q_y,q_z), $$

where $$ f_\bot(q_y,q_z) = Hi\frac{\text{e}^{-i q_y d}}{q_y} \left[ \text{e}^{i \alpha_{-}/2} \text{sinc}\left( \frac{\alpha_{+}}{2} \right) - \text{e}^{i \alpha_{+}/2} \text{sinc}\left( \frac{\alpha_{-}}{2} \right) \right], $$

with the notation $$ \alpha_{+} = H q_z + \frac{q_y W}{2} + q_y d, \quad \alpha_{-} = H q_z - \frac{q_y W}{2} + q_y d. $$

Corresponding factor $ f_\parallel(q_x) $ is chosen according to longitudinal profile.

Volume has been validated against $$ V=\dfrac{LWH}{2}. $$

Scattering

Scattering by uncorrelated, oriented sawtooth ripples for horizontal incidence. Rotation around $z$ axis:

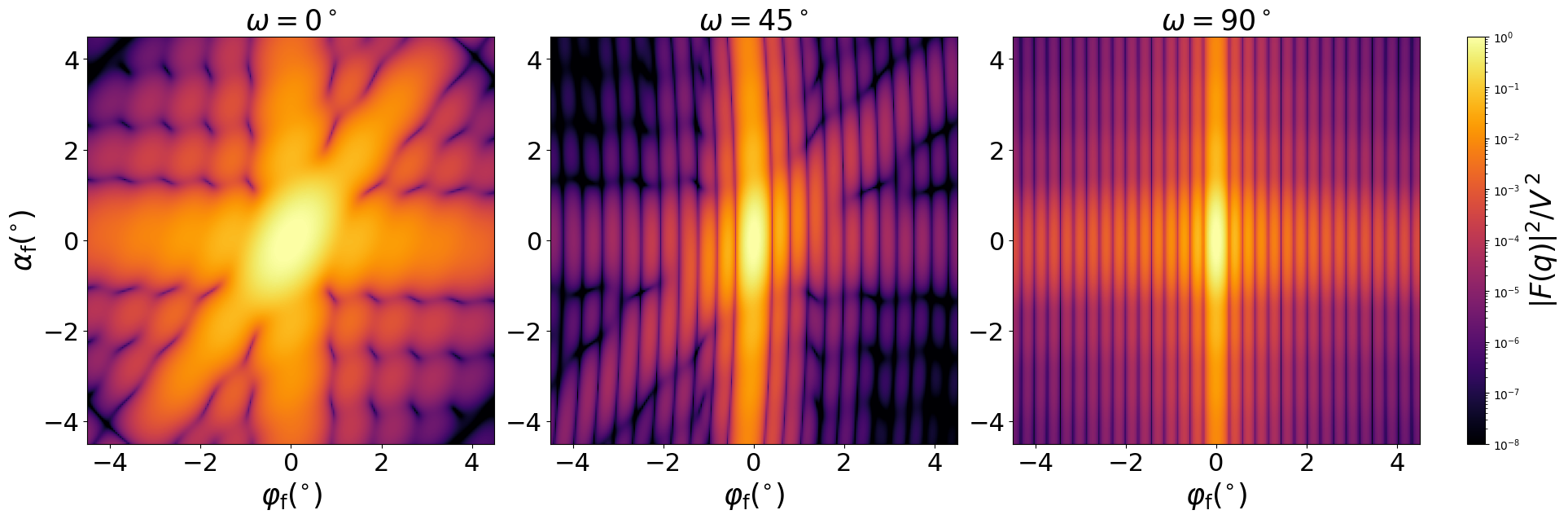
Generated by Examples/ff/SawtoothRippleBox.py .

History

“SawtoothRippleBox” replicates “Ripple2” from FitGISAXS [Babonneau 2013].