 BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ Pyramid3
BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ Pyramid3
A truncated pyramid (frustum) with trigonal base.



Pyramid3(L, H, alpha)
Parameters:
Constraint:
$H \le \dfrac{\tan\alpha}{2\sqrt3} L$
The orthographic projection also shows the angle $\beta$ between the base and a side edge. It is related to the dihedral angle through $\tan\alpha = 2\tan\beta$.
As for any other Form factor.
Class Pyramid3 inherits from the interface class IFormfactor .
Form factor computation is based on the generic form factor of a polyhedron provided by libformfactor .
Volume has been validated against $$ V=\dfrac{L^3\tan\alpha}{24}\Big[1-\Big(1-\dfrac{2\sqrt3H}{L\tan\alpha}\Big)^3\Big]. $$
More special:
Scattering by uncorrelated, oriented pyramids for horizontal incidence. Rotation around $z$ axis:
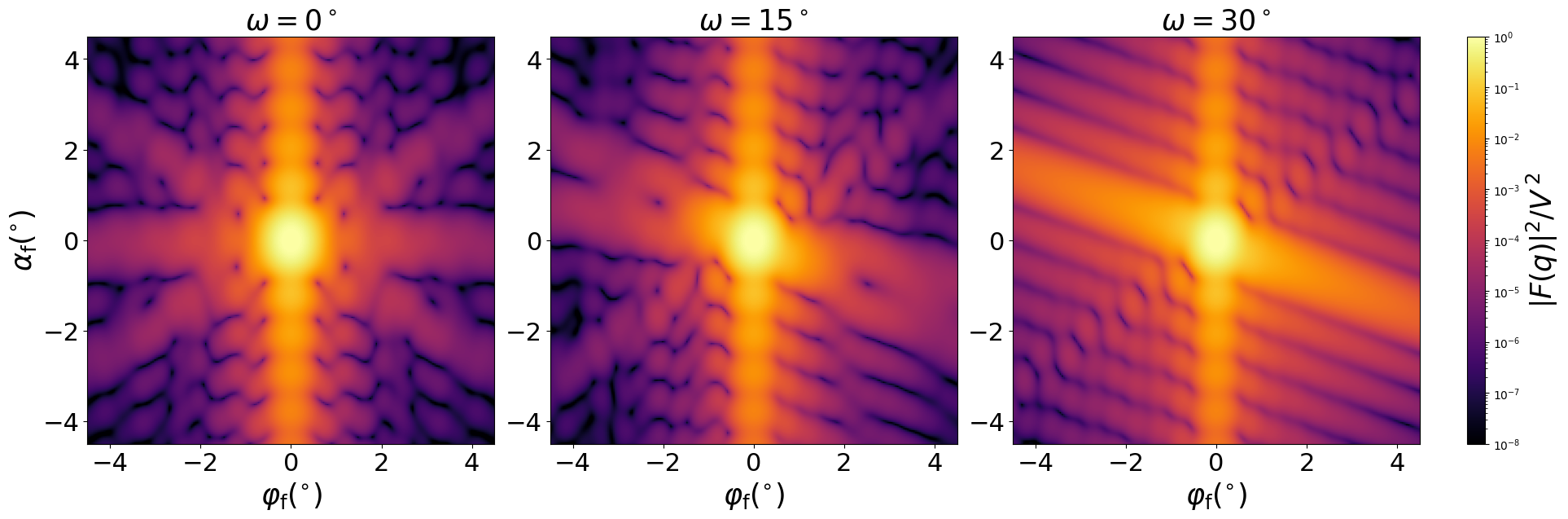
Generated by Examples/ff/Pyramid3.py .
Was incorrectly named “Tetrahedron” up to BornAgain 1.19.
Corresponds to “Tetrahedron” in IsGISAXS [manual, Eq. 2.29; Renaud 2009, Eq. 220] and “Truncated tetrahedron” in FitGISAXS [Babonneau 2013]. In BornAgain 1.6, redefined to let the $x$ axis lie in a mirror plane (rotated by $30^{\circ}$ with respect to the previous version).
Up to BornAgain 1.5, we computed the form factor by numeric integration, as in IsGISAXS. Since BornAgain 1.6 higher speed and accuracy are achieved by using the generic form factor of a polyhedron [Wuttke 2021] with series expansions near singularities.