BornAgain ≻ git-main ≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ Spheroid

Spheroid

A full spheroid, generated by rotating an ellipse around the vertical axis.

Constructor

Spheroid(R_xy, R_z)

Parameters:

  • $R_{xy}$, horizontal radius
  • $R_z$, vertical radius

Attention This has changed in BornAgain 22. Previously, the second argument was $H=2R_z$.

Usage

As for any other Form factor.

Implementation

Class Spheroid inherits from the interface class IFormfactor.

Form factor is computed as

$$ F(\mathbf{q})=4\pi R_{xy}^2R_z \exp(iq_zR_z) \dfrac{\sin(s) - s \cos(s)}{s^3} , $$ with the notation $$ s := \sqrt{(R_{xy}q_x)^2 + (R_{xy}q_y)^2+ (R_zq_z)^2}. $$

Volume has been validated against $$ V=\dfrac{4\pi}{3} R_{xy}^2R_z. $$

More special:

More general:

Example

Scattering by uncorrelated, oriented spheroids for horizontal incidence. Rotation around $y$ axis:

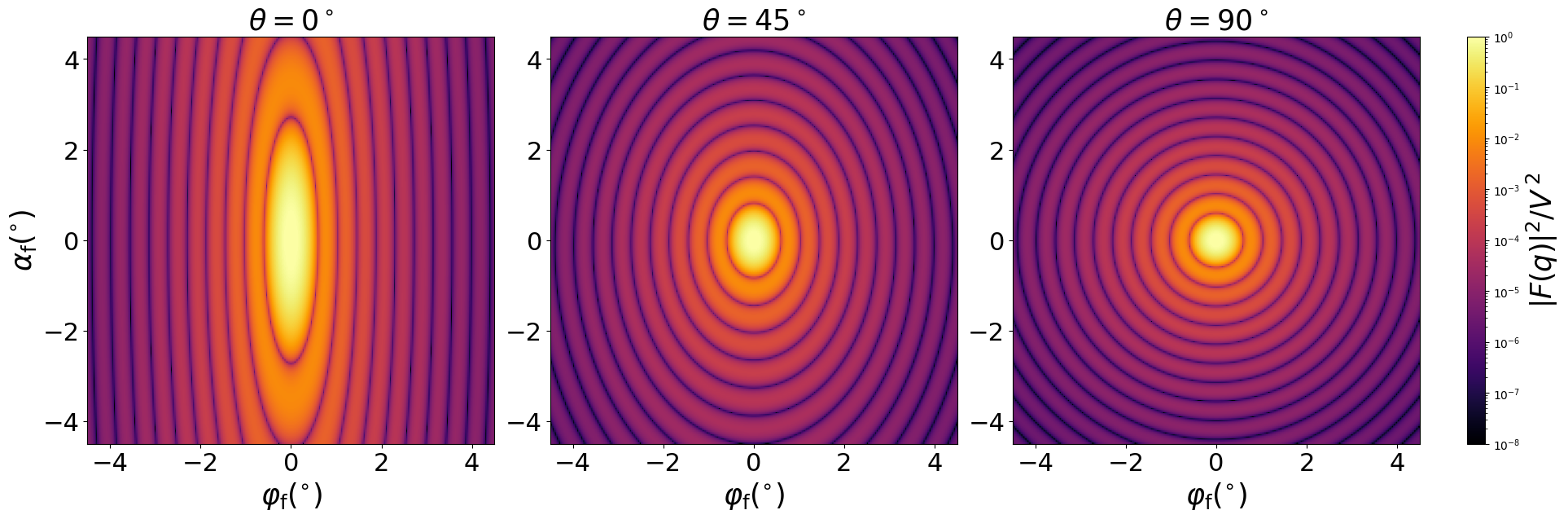
Generated by Examples/ff/Spheroid.py .

History

Replicates the “Full spheroid” in IsGISAXS [manual, Eq. 2.36; Renaud 2009, Eq. 227], except for wrong factors of 2 in their volume formula and form factor implementation, and “Spheroid” in FitGISAXS [Babonneau 2013]. Up to BornAgain 1.16, our form factor computation followed IsGISAXS in using numeric integration in the $z$ coordinate.

In BornAgain, named “FullSpheroid” up to version 1.19.

Up to BornAgain 21, the second argument was $H=2R_z$.