 BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ TruncatedSpheroid
BornAgain
≻ git-main
≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ TruncatedSpheroid
A vertically oriented, horizontally truncated spheroid.



TruncatedSpheroid(R, H, f_p, dh)
Parameters:
Constraint:
$ dh < H \le 2f_pR $
As for any other Form factor.
Class TruncatedSpheroid inherits from the interface class IFormfactor .
Computation involves numerical integration in vertical direction,
$$ F(\mathbf{q})=2\pi \exp[iq_z(H-f_pR)] \int_{f_pR-H}^{f_pR-dh} \text{d}z \space R_z^2 \frac{J_1(q_{||}R_z)}{q_{||}R_z} \exp(iq_z z), $$
with the notation
$$ q_{||} := \sqrt{q_x^2 + q_y^2}, \quad R_z:=\sqrt{R^2-z^2/f_p^2} $$
Volume has been validated against $$ V=\dfrac{\pi}{3f_p^2} [ 3f_pR(H^2-dh^2) + dh^3 -H^3 ]. $$
More special:
Scattering by uncorrelated, oriented truncated spheroids for horizontal incidence. Rotation around $y$ axis:
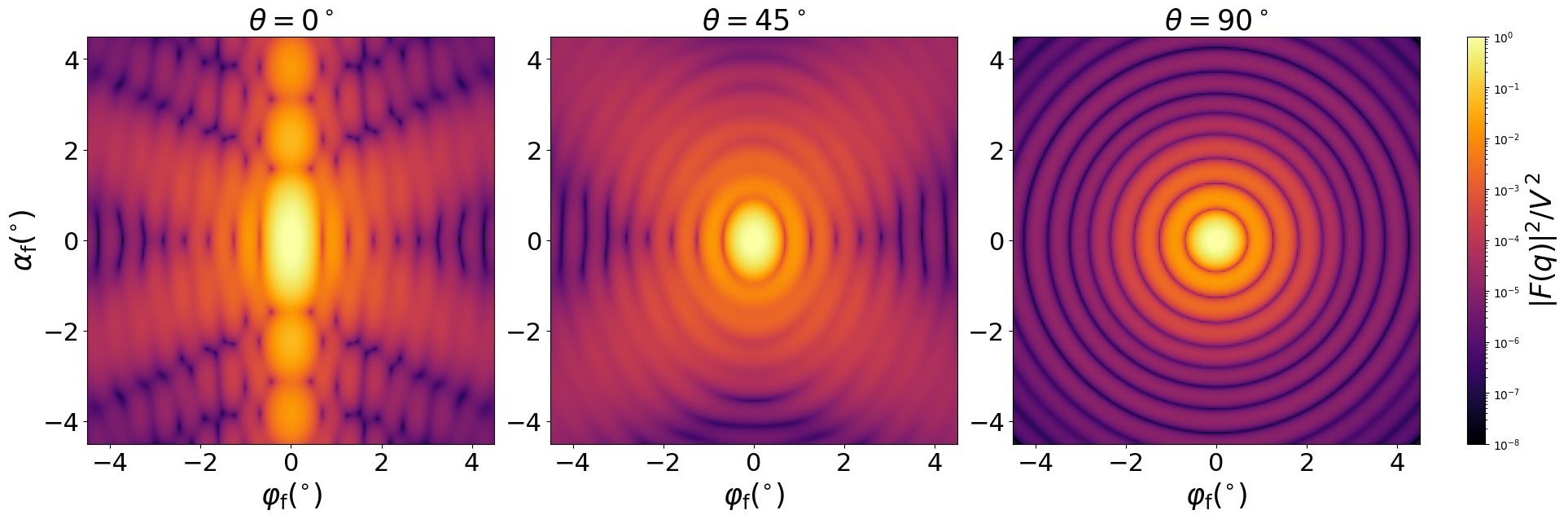
Generated by Examples/ff/TruncatedSpheroid.py .
Agrees with the IsGISAXS form factor “Spheroid” [manual, Eq. 2.42].