BornAgain ≻ git-develop ≻ Documentation ≻ Reference ≻ Sample model ≻ Particles ≻ Form factor ≻ Hard particles ≻ EllipsoidalSegment

EllipsoidalSegment

A horizontally truncated ellipsoid.

Constructor

EllipsoidalSegment(R_x, R_y, R_z, t, b)

Parameters:

  • R_x, radius $R_{x}$ in $x$ direction
  • R_y, radius $R_{y}$ in $y$ direction
  • R_z, radius $R_{z}$ in $z$ direction
  • $ t $, cut from top
  • $ b $, cut from bottom

Usage

As for any other Form factor.

Implementation

Class EllipsoidalSegment inherits from the interface class IFormfactor.

Computation involves numerical integration in vertical direction,

$$ F(\mathbf{q})=2\pi \exp[iq_z(R_z-b)] \int_{-R_z+b}^{R_z-t} \text{d}z \space r_{x,z} r_{y,z} \frac{J_1(\gamma_{z})}{\gamma_{z}} \thinspace \exp(iq_z z) , $$

with the notation

$$ r_{x,z}:=R_{x}\sqrt{1-\Big( \dfrac{z}{R_z} \Big)^2}, \quad r_{y,z}:=R_{y}\sqrt{1-\Big( \dfrac{z}{R_z} \Big)^2}, $$

$$ \quad \gamma_{z} := \sqrt{(q_xr_{x,z})^2 + (q_yr_{y,z})^2}. $$

Volume has been validated against $$ V=\dfrac{\pi}{3} \frac{R_{x}R_{y}}{R_z^2} [ 4R_z^3 - 3R_z(t^2+b^2) + (t^3 + b^3) ]. $$

More special truncated shapes:

More special full shapes, if $t=b=0$:

Example

Scattering by uncorrelated, oriented truncated ellipsoids for horizontal incidence. Rotation around $z$ axis:

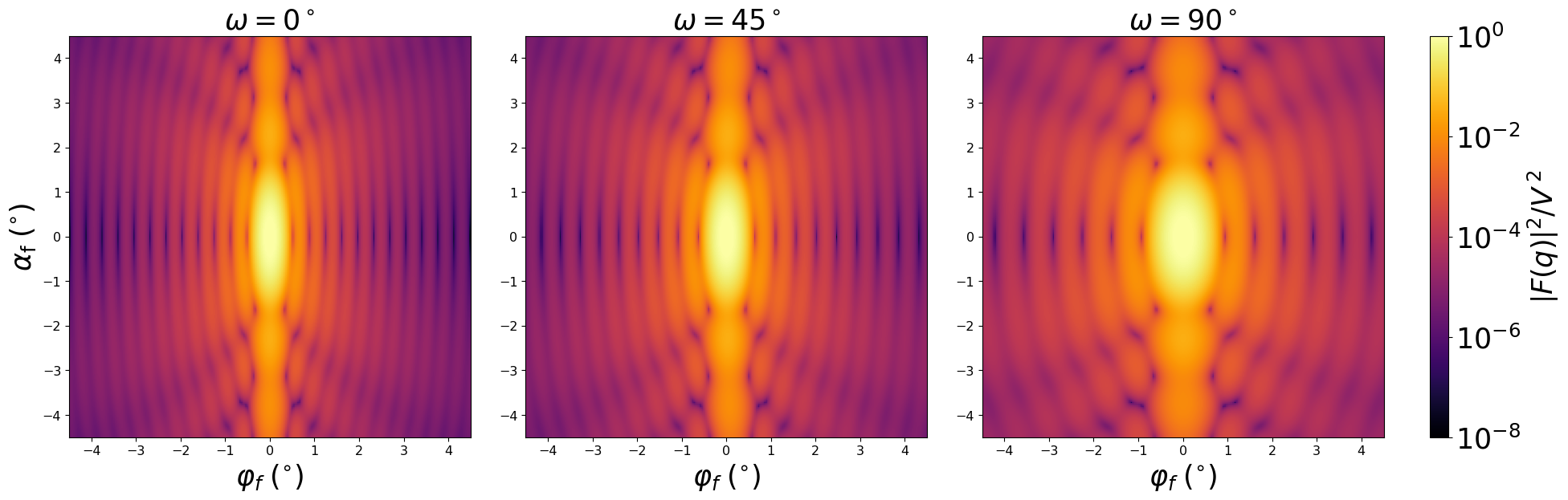
Generated by Examples/ff/EllipsoidalSegment.py .

History

Up to v23 the formfactor “HemiEllipsoid” was used, which agreed with the IsGISAXS form factor “Anisotropic hemi-ellipsoid” [manual, Eq. 2.41] with wrong sign in the z-dependent phase factor and “Hemi-spheroid” [Renaud 2009, Eq. 229].